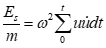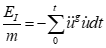Session 1: Special Sessions: CC 10. Dynamics, Control, and Identification of Structural Systems

Force and displacement-based methodologies are generally proposed by modern seismic design codes. In the force-based analyses, the equivalent earthquake loads are reduced by a factor “R”, which relies on the ductility and over-strength factor of the structure. At the end of the design procedure, the structural members are expected to carry those reduced loads safely. However, the deformation intensities and their distribution on the structural system are not clear. The displacement-based methods use the structural capacity curve to compute the displacement demand of the structure. Member deformations are determined and classifed by comparing these against some reference values. However, the effective duration and frequency content of the earthquake (EQ) and the hysteretic behavior of structural members are disregarded in this methodology. It was also stated that displacement-based procedures have difficulty in accounting for the duration-related damage, in a similar manner to force-based methodologies (Chou and Uang, 2000). Hence, a more comprehensive design methodology named as “Energy Based Seismic Design” (EBSD) was proposed, originally by Housner (1956). It takes into account frequency content and duration of the EQ and hysteretic behavior of the structural members rather than envelope curves. Additionally, energy is a scaler value whereas force and displacement are vector terms. Therefore combination effects of orthogonal directions might be minimized. Moreover, seismic energy account for cumulative effects of both force and deformation whereas displacement procedures consider pay attention for only the maximum values.

After introducing by Housner (1956); energy balance equation in time domain, that based on equation of motion of a single degree of freedom system (SDOF), derived by Akiyama (1985). It was also shown in the literature that mass normalized seismic input energy can be expressed in spectral form.

Determination of the mass normalized seismic energy  (EI/m) spectrum necessitates tedious and time consuming calculation efforts. However, some analyses tecniques exists in the literature that enable the analysis of SDOF systems. One of them is the piece-wise exact method proposed by Aydınoğlu and Fahjan (2003). It is capable of acounting for the geometric nonlinearity.The originally proposed method to obtain seismic response of SDOF systems, is utilized here as a tool in the determination of the EI/m spectrum. Even though the original method is able to consider two different constitutive equations, Elastic Perfectly Plastic (EPP) response model has been utilized in the developed algorithm depending on the conclusions that the hysteretic model type is ineffective on the seismic input energy (Benavent-Climent 2010, Dindar et al. 2015).

Restoring force of the system can be rewritten as given in Eq. 1.

Where β_ej is effective stiffness coefficient of the linear segment in terms of the initial stiffness, ω is circular frequency of the SDOF system, f_s is restoring force, m is mass, u.. is relative acceleration, u. is relative velocity, u is relative displacement, and u^g is ground acceleration. The ground acceleration can also reexpressed as a linear function between the time steps. Solution of the equation has two parts namely complementary solution corresponding to the free vibration response of system and particular solution that satisfies right hand side of the equation. The solutions were given for possitive, negative and zero effective stiffnesses in Aydınoğlu and Fahjan (2003). Moreover displacement and velocity of the system at the time step of t_i+1 was obtained as given in Eqs. 2 and 3. The acceleration response of the system can be computed simply through derivating the velocity.

Since the structural responses are determined, seismic input energy and its components are computed by Eqs. 4 to 7.

Where E_k is kinetic energy, E_D is damping energy and E_s is strain energy.

The MATLAB based code (PW-SPECTs) is generated for the algorithm developed in the content of this paper. The input data of the code are the vibrational period, damping ratio, time span and ground motion data. The code not only produces the responses and the energy histories but also their spectral counterparts. The tested SDOF and MDOF systems with diverse vibrational and damping properties are used for the verification of PW-SPECTs. 

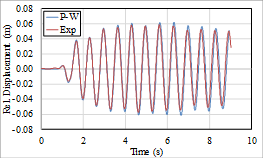
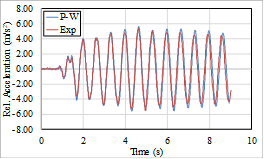
The extended algorithm firstly verified by the experimental results in terms of relative displacement, velocity and acceleration responses of a SDOF system tested on shake table, Fig. 1.

Fig. 1: PW-Spect vs experimental results in terms of relative top responses

Since the algorithm successfully computed the response of a SDOF system having a specific vibrational period; displacement, velocity and acceleration spectra of a spefic record computed by PW-SPECTs and Seismo Signal was compared in Fig. 2. The results were consistent with each other.

Fig. 2: Spectra computed by PW-SPECTs and SeismoSignal

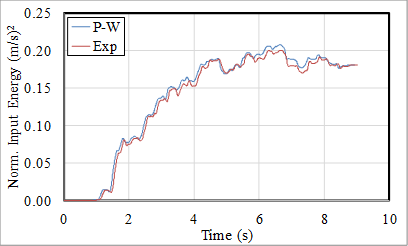
In the third phase of the verification, experimentally obtained mass normalized seismic input energy history of a SDOF specimen having 0.667 s vibrational period and 0.3% damping ratio was compared with PW-SPECTs. The results were almost identical.

Fig. 3: Mass normalized seismic input energy computed by experimental results and PW-SPECTs

Since there were not commercial software for computing seismic energy spectra, the seismic energy spectra computed by PW-SPECTs were compared with the 10 discrete SDOF specimens with diverse natural vibrational periods. The black dots in the figure corresponds to the seismic energy computed from the experimental results whereas the blue solid line corresponds to prediction of PW-SPECTs. 

Fig. 4: Piece-wise exact method vs. experimental results in terms of seismic energy

The numerical spectrum makes relatively good estimations for the experimental results.

Close form solution of the energy balance equation depending on piece-wise exact method is proposed here. The developed algorithm is an efficient tool to obtain both seismic input energy history and spectra in a very short time without tedious processes. Therefore it can be utilized as a practical tool for the developed or will be developed seismic energy based procedures.

References:

Akiyama, H. (1985). Earthquake-Resistant Limit-State Design for Buildings. University of Tokyo Press.

Aydınoğlu, N., Fahjan, Y.M. (2003). A unified formulation of the piecewise exact method for inelastic seismic demand analysis including the P-delta effect. Earthquake Engng Struct. Dyn., 32:871-890.

Benavent-Climent, A., Zahran, R. (2010) An energy based procedure for the assessment of seismic capacity of existing frames: application to RC wide beam systems in Spain. Soil Dynamics and Earthquake Engineering, 30:354-367

Chou, C.C., Uang, C.M. (2000). Establishing absorbed energy spectra – an attenuation approach. Earthquake Engineering and Structural Dynamics, 29(10):1441-1455.

Dindar, A.A., Yalçın, C., Yüksel, E., Özkaynak, H., Büyüköztürk, O. (2015). Development of earthquake energy demand spectra. Earthquake Spectra, 31(3):1667-1689.

Housner, G.W. (1956). Limit design of the structures to resist earthquakes. Proceedings of the 1st World Conference on Earthquake Engineering. Berkeley: California.

SeismoSoft (2016) SeismoSignal

Seismic energy balance concept firstly introduced by Housner (1952) and then Akiyama (1985) obtained energy balance equation in time domain that based on the equation of motion of a single degree of freedom system (SDOF).

Energy based seismic design considers both force and deformation while accounting for the influence of cumulative damage. In contrary, displacement based design methods pay attention for only the maximum values.

Determination of the E_I/m spectrum necessitates vast and time consuming calculation efforts. However, some analyses tecniques exists in the literature that enable the analysis of SDOF systems such as piece-wise exact method. It is capable of acounting for the geometric nonlinearity.The method that was originally proposed to obtain seismic response of SDOF systems, is utilized here as a tool in the determination of the E_I/m spectrum. The original method is able to consider two different constitutive equations. In the algorithm developed in this paper, the Elastic Perfectly Plastic (EPP) response model has been utilized, depending on the conclusions that the hysteretic model type is ineffective on the seismic input energy.

The MATLAB based code PW-SPECTs is generated for the algorithm developed in the content of this paper. The input data of the code are the vibrational period, damping ratio, time span and ground motion data. The code not only produces the responses and the energy histories but also their spectral counterparts. The tested SDOF and MDOF systems with diverse vibrational and damping properties are used for the verification of PW-SPECTs.

Close form solution of the energy balance equation depending on piece-wise exact method is proposed here. The developed algorithm is an efficient tool to obtain both seismic input energy history and spectra in a very short time without tedious processes.

Vibration serviceability often governs the dynamic design of pedestrian structures, such as footbridges, large-span floors, staircases, etc. Reliable prediction of pedestrian-induced vibrations is essential to the vibration serviceability evaluation in the design stage. 

Till now, many efforts have been devoted to obtaining reliable evaluation of the vibration serviceability of pedestrian structures. Many models are developed in the domain of pedestrian-induced vibrations of pedestrian structures. 

However, in currently available models, simplifying assumptions are often adopted in aspects as follows: (1) modal properties of structures are assumed constant in the structural system identification; (2) effects of pedestrian-structure interaction are not considered or considered based on linear dynamic behaviour of pedestrian body; (3) walking parameters and pedestrian-induced walking forces are assumed to be same for all individuals and thus without considering inter- and intra-subject variabilities.  

In this contribution, some aspects of these simplifying assumptions are evaluated in the context of pedestrian-induced vibrations of pedestrian structures.  

Extensive field tests are carried out on a real-world staircase. Firstly, linear sweep tests are applied to identify the modal properties of the staircase. In the system identification procedures, modal masses of the structure are assumed constant. The effective natural frequencies and modal damping ratios for each mode of the structure are obtained from a least-square fit between the measured structural responses and the calculated acceleration responses of an equivalent SDOF system of the considered mode. In the response calculations, the equivalent SDOF system is subjected to the measured excitation forces in terms of the relative acceleration of the shaker mass. 

Next, to identify the dynamic properties of the pedestrian body, the empty structure is excited by the shaker at the fundamental natural frequency of the structure. In this stage, the structural response is totally dominated by the fundamental mode of the structure. After the structure reaches full steady response (as the background signal for the measurements), the pedestrian starts walking on the staircase at a specific step frequency, which is not the same as the resonant frequency. Also, the integer multiple of the step frequency should not meet the resonant frequency. This makes it possible to identify the dynamic properties of the pedestrian body. Practically, it is possible to be separated the response to the background excitation from the pedestrian-induced vibration in the observed structural responses. 

In the measurements when the pedestrian is passing the structure, the structural acceleration responses are recorded. Also, the time-variant position of the crossing person is monitored. In the calculations of the pedestrian-induced vibrations, the pedestrian body is represented by a SDOF system with the pedestrian mass as the sprung mass and to-be-identified natural frequency and damping ratio of the pedestrian body. The SDOF system of the human body is moving along the structure in accordance with the registered positions of the person. The dynamic properties of the pedestrian body are identified based on the good agreement between the measured and calculated acceleration responses of the coupled pedestrian-structure interaction system in time domain. A moving discrete Fourier transform (DFT) over a time window of 10 s is applied in the identification procedures. 

The natural frequency and damping ratio of pedestrian structures are identified to be amplitude-dependent. Also, dynamic properties of the pedestrian body are found nonlinear. Based on the findings from the investigations in this contribution, the assumed linear dynamic behaviour of the structure in the system identification procedures results in inaccuracy of the identification of the modal properties (natural frequencies and damping ratios) of the structure. The inaccurately identified modal properties of the structure further cause the inaccuracy of the identified pedestrian body dynamics based on the coupled pedestrian-structure interaction system.       

Results from this study show that simplifying assumptions of the modal properties of the structure and the pedestrian body dynamics both result in the inaccurate predictions of human-induced vibrations of pedestrian structures. In addition, the inaccurately identified modal properties of the structure add more difficulties in the identification of the nonlinear pedestrian body dynamics.

Vibration serviceability often governs the dynamic design of pedestrian structures. Reliable prediction of pedestrian-induced vibrations is essential to the vibration serviceability evaluation in the design stage. Many models have been developed to evaluate vibration serviceability of pedestrian structures under human excitations. However, among these models, simplifying assumptions are often adopted as follows: (1) modal properties of structures are assumed constant in the structural system identification; (2) effects of pedestrian-structure interaction are not considered or considered based on linear dynamic behaviour of pedestrian body; (3) inter- and intra-subject variabilities in walking parameters and walking forces are neglected or not fully considered.  

To address some aspects of these simplifying assumptions, extensive field tests are carried out on a staircase. Firstly, linear sweep tests are applied to identify the modal properties of the staircase. The effective natural frequencies and damping ratios are obtained from a least-square fit between the measured structural responses and the calculated acceleration responses of an equivalent SDOF system. In the response calculations, the equivalent SDOF system is subjected to the measured shaker excitation forces. Next, to identify the dynamic properties of the pedestrian body, the empty structure is excited by the shaker at the fundamental natural frequency. After the structure reaches full steady response, the pedestrian starts walking on the staircase at a specific step frequency. In the measurements when pedestrian passing, the structural acceleration responses are recorded. Also, the time-variant position of the crossing person is monitored. In the calculations of the pedestrian-induced vibrations, the pedestrian body is represented by a SDOF system. The SDOF system of the human body is moving along the structure in accordance with the registered positions of the person. The dynamic properties of the pedestrian body are identified based on the good agreement between the measured and calculated acceleration responses of the coupled pedestrian-structure interaction system in time domain. A moving discrete Fourier transform (DFT) over a time window of 10 s is applied in the identification procedures.

Results show that the modal parameters of the staircase are identified to be amplitude-dependent. Dynamic properties of the pedestrian body are found nonlinear. It also shows that the assumed linear dynamic behaviour of the structure in the system identification procedures results in inaccuracy of the identification of the modal properties of the structure. The inaccurately identified modal parameters further cause the inaccuracy of the identified pedestrian body dynamics based on the coupled pedestrian-structure interaction system.

Applied system identification can be seen as the complex process of developing mathematical models of dynamical systems based on input-output data. In general, a mathematical model of a physical system can be used to predict by means of numerical simulations the system dynamic behavior in response to known external excitations. In the field of applied system identification, the basic laws of mechanics are combined with statistical methods in order to devise mathematical models of dynamical systems by using experimental measurements. Model reduction techniques and the methodologies for the optimal design of experiments are also widely employed in the field of applied system identification. In this context, numerical experiments obtained by means of dynamic simulations can be performed by using a reliable mathematical model of a physical system in order to reproduce the input-output relationships observed experimentally. This work in grounded in the field of the computational methods of applied system identification that are used for estimating the modal parameters of structural and mechanical systems. In particular, this investigation deals with the development of a system identification numerical procedure based on time-domain data which can be effectively used for obtaining time-invariant dynamical models of mechanical systems having a linear structure. For a general mechanical system, the state-space model identified by means of the numerical algorithm discussed in this paper can be employed for describing the system input-output mapping as well as for computing the system natural frequencies, damping ratios, and mode shapes. Furthermore, the computational approach discussed in this work can be effectively applied in the field of vehicle system dynamics for identifying simple dynamical models useful for the development of optimal control strategies.

The numerical methods considered in this paper are the ERA/OKID algorithms (Eigensystem Realization Algorithms/Observer-Kalman Filter Identification Methods) and the N4SID methods (Numerical Algorithms for Subspace State-Space System Identification). This section presents the identification systems of the state-space matrices of the first order of OKID and N4SID, and the methodology for tracing back to the second-order mechanical model. A system identification methodology can be developed using the combination of the Markov parameters of the identified system and the Markov parameters of the observer gain. In particular, the generalized Hankel matrix can be easily resized using the decomposition of singular values (SVD). An in-depth analysis of the spectrum of singular values of the generalized Hankel matrix allows us to establish the order of the identified space-state model. In this way, it is possible to calculate a discrete-time space-state model that leads to discrete-time space-state matrices and also to the matrix of the identified observer.

The system identification numerical procedures of interest for this investigation are systematically compared by means of numerical experiments and employing experimental measurements taken on a vibrating system. The first demonstrative example is a dynamical model of a two-degrees-of-freedom lumped-parameter mechanical system. This demonstrative example is used in a virtual environment for assessing the quality of the results identified by using the ERA/OKID method and the N4SID technique in the presence of an artificial noise on the input and output measurements. On the other hand, the mechanical system considered as the second demonstrative example of the approach developed in the paper is a three-dimensional flexible structure that forms a simple test rig. The flexible structure used as a test rig can be modeled as a three-story shear building system. The structural system is composed of six flexible beams and three rigid connecting rods. The flexible beams are made of harmonic steel while the material of the connecting rods is aluminum. The dynamic behavior of the mechanical system considered as a case study is of interest for this investigation and serves as a test rig for studying the mechanical vibrations of real full-scale flexible structures subjected to the earthquake. For this purpose, the frequency range of interest for this study includes all the excitation frequencies between 0 (Hz) and 15 (Hz). In this frequency range, the flexible beams deform as linear elastic continuum bodies and the connecting rods behave essentially as rigid bodies. Observing the geometric configuration of the three-story system, this flexible structure is deployed in a plane. Therefore, the lateral stiffness and the torsional stiffness of the flexible structure are considerably larger than stiffness along the plane. Consequently, this three-dimensional flexible structure can be modeled as a planar three-story shear building system with a very good approximation. The first floor of the flexible structure is excited by a shaker that is connected to the structure by means of a stinger. A load cell is collocated between the first floor and the stinger in order to measure the force transferred to the flexible structure by the shaker. In order to minimize the inertial influence of the shaker on the flexible structure, the shaker is suspended through a steel cable fixed on external supports that are isolated from the flexible structure of interest. The shaker is connected to a power amplifier which is controlled by an arbitrary wave function generator. In order to measure the time response of the three-story shear building system, piezoelectric transducers that sense the system accelerations are collocated on each floor of the flexible structure. An experimental modal analysis of the flexible structure was performed at first. To this end, the three floors of the flexible structure were excited by using an impact hammer instrumented with a load cell connected to a spectrum analyzer. The proposed identification procedure was applied to the set of input-output data obtained by means of experimental measurements. Subsequently, the identified discrete-time state-space matrices representing the identified linear dynamical model of the flexible structure and the identified observer matrix were computed by means of the ERA/OKID technique and the N4SID method yielding to a set of identified modal parameters that basically contains the identified natural frequency of a given normal mode and the identified damping ratio corresponding to the same normal mode. It is important to note that the modal parameters of the identified continuous-time state-space model are consistent with those obtained by using the preliminary lumped parameter model. Since the identified modal damping is small, the identified mode shapes are approximately in phase or out of phase. Therefore, the hypothesis of proportional damping can be assumed and the proposed method for identifying the proportional damping coefficients can be applied.

In this paper, a numerical and experimental comparison between the ERA/OKID methods and the N4SID algorithms is proposed. Both families of methodologies allow for performing the time-domain state-space system identification, namely, they lead to an estimation of the state, input influence, output influence, and direct transmission matrices that characterize the dynamics of a discrete-time mechanical system. The present investigation demonstrates that, if properly tuned, both the ERA/OKID methods and the N4SID algorithms lead to consistent numerical results, even in the case when the input-output measurements used for performing the identification procedure are affected by a certain degree of noise. Furthermore, in this work, a least-square method is proposed for reconstructing an improved estimation of the damping matrix starting from a triplet of estimated mass, stiffness, and damping matrices of a linear mechanical system.

In this work, two identification methods are used and compared for performing the experimental modal analysis of a structural system. The identification procedures considered are the ERA/OKID algorithms (Eigensystem Realization Algorithms/Observer-Kalman Filter Identification Methods) and the N4SID methods (Numerical Algorithms for Subspace State-Space System Identification). These identification techniques are implemented in the Matlab/Simulink environment and are based on the numerical methods of dynamic identification developed in the domain of time. The case study considered in this paper is a flexible structure that can be modeled as a three-story structural system. A preliminary mechanical model of the flexible structure is developed using a lumped-parameter approach. Subsequently, a more realistic finite element model is built starting from the three-dimensional CAD geometry of the structural system under consideration. The two preliminary mechanical models are employed for the modal analysis of the actual structure and are useful to trace guidelines and evaluate the effectiveness of the experimental identification results. In particular, the two identification methods allow for identifying a first-order state-space model by directly starting from the experimental data measured in input and output on the system. From the identified first-order dynamical model, a second-order mechanical model of the flexible structure is obtained, which is useful in various fields of both mechanics and control. In the second dynamic model obtained from experimental data, considering the hypothesis of proportional damping, an effective method is used to calculate an improved estimation of the identified damping coefficients. The numerical and experimental results found in this study confirmed the effectiveness of the methodologies used.